Table of Contents
- Types of Supports and Their Reactions
- A Step-by-step Guide on Determining the Support Reactions in Beams
- SkyCiv Beam Software
Types of Supports and Their Reactions
In this article, we discuss reaction force formula and how to find support reactions. First, it’s important to also understand the different types of supports and what reactions they produce in your analysis model. Below is a short cheat sheet of the different support types and their reactions:
| Type of Support | Translation | Rotation | Notes |
|---|---|---|---|
Fixed Support |
Fixed in all directions Reactions in X,Y,Z |
Fixed in all directions Reactions in X,Y,Z |
FFFFFF – Reactions in all degrees of freedom |
Horizontal Roller Support |
Fixed in Y Reactions in Y direction only |
Released in all Directions No rotational reactions |
RFFRRR – Reactions are only in the Y direction |
Pinned or Hinged Support |
Fixed in X,Y,Z Reactions in X,Y,Z |
Released in all Directions No rotational reactions |
FFFRRR – Reactions in all translation, none in rotation |
Cantilever Support |
Fixed in all directions Reactions in X,Y,Z |
Fixed in all directions Reactions in X,Y,Z |
Same as fixed |
A Step-by-step Guide on Determining the Support Reactions in Beams:
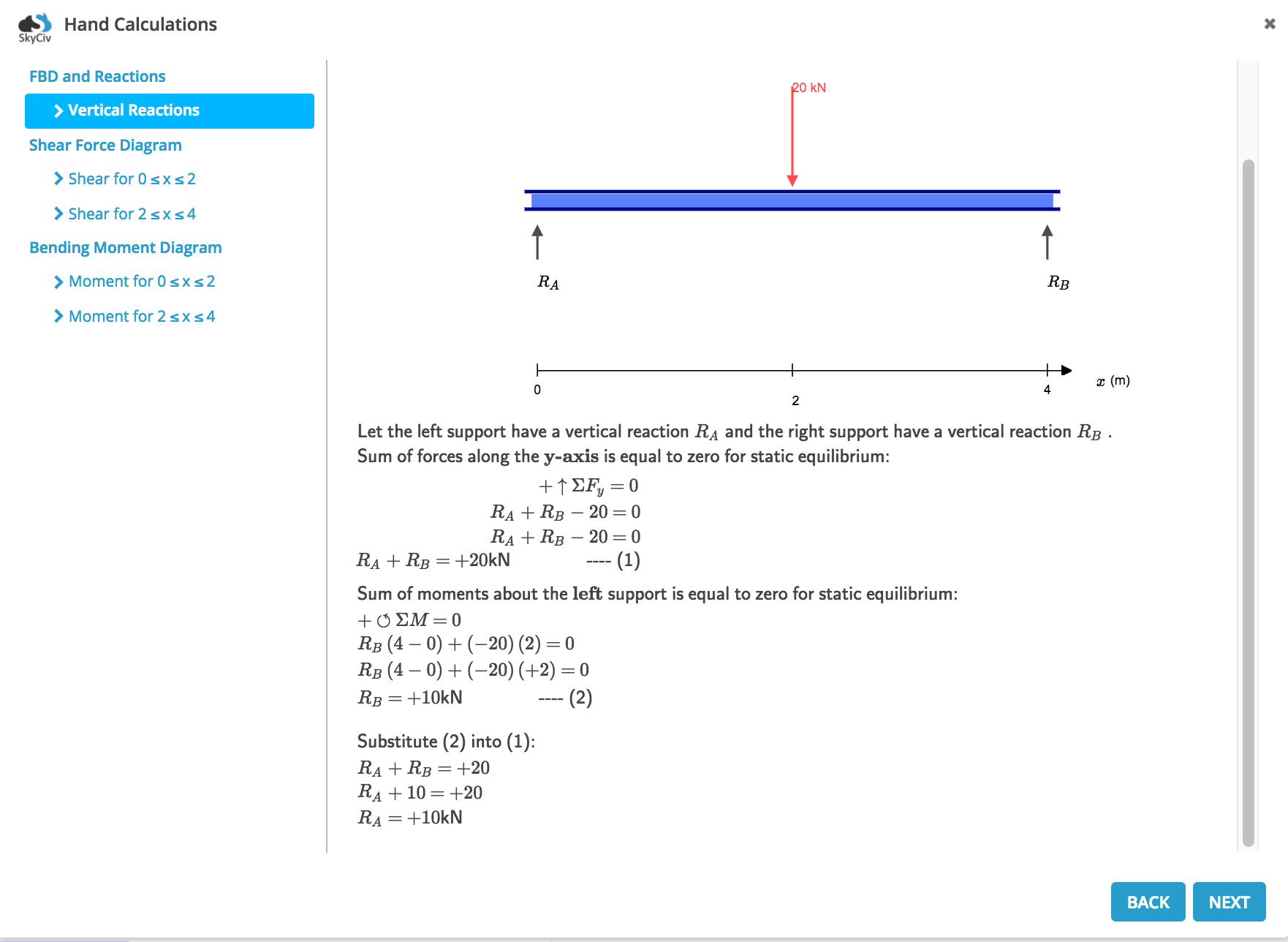
Determining reactions at supports is always the first step in analyzing a beam structure, and it is generally the easiest. It involves calculating the reaction forces at the supports (supports A and B in the below example) due to the forces acting on the beam. You will need to know this to progress through and calculate bending moment diagrams (BMDs) and shear force diagrams (SFDs); an important part of your statics and structural college/university courses. SkyCiv offers a powerful Free Reaction Calculator that allows you to model any beam and show these hand calculations for you, but it is also an important concept to understand.
Video tutorial: Determine the reactions at the supports
When solving a problem like this we want to first remember that the beam is static; meaning it is not moving. From simple physics, this means that the sum of the forces in the y-direction equals zero (i.e. the total downward forces equal the total upward forces). A second formula to remember is that the sum of the moments about any given point is equal to zero. This is because the beam is static and therefore not rotating.
To determine the reactions at supports, follow these simple steps:
1. Sum of Moments (ΣM = 0)
All we need to know about moments at this stage is that they are equal to the force multiplied by the distance from a point (i.e. the force x distance from a point). Consider a simple example of a 4m beam with a pin support at A and roller support at B. The free-body diagram is shown below where Ay and By are the vertical reactions at the supports: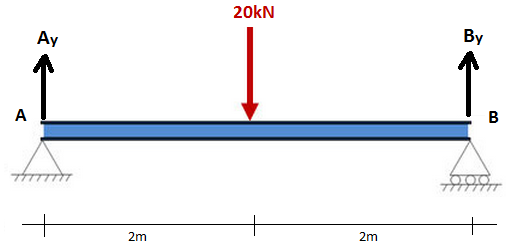
We first want to consider the sum of moments about point B and let it equal zero. We have chosen point B to prove this can be done at either end of the beam (provided it is pin supported). However, you could just as easily work from point A. So, now we sum the moments about point B and let the sum equal 0:
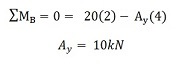
NOTE: The sign convention we have chosen is that counter-clockwise moments are positive and clockwise moments are negative. This is the most common sign convention but it is up to you. You must ALWAYS use the same sign convention throughout the whole problem. Always use the same sign convention from the start. We now have our first equation. We need to solve another equation in order to find By (the vertical reaction force at support B).
2. Sum of Horizontal Forces (ΣFy = 0)
Sum the forces in the y (vertical) direction and let the sum equal zero. Remember to include all forces including reactions and normal loads such as point loads. So if we sum the forces in the y-direction for the above example, we get the following equation:
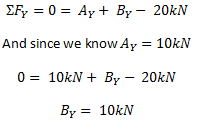
NOTE: Again we stuck to a sign convention which was to take upward forces (our reactions) as positive and downward forces (the point load) as negative. Remember the sign convention is up to you but you must ALWAYS use the same sign convention throughout the whole problem.
So there we have it, we have used the two above equations (sum of moments equals zero and sum of vertical forces equals zero) and calculated that the reaction at support A is 10 kN and the reaction at support B 10kN. This makes sense as the point load is right in the middle of the beam, meaning both supports should have the same vertical forces (i.e. it is symmetric).
In summary, here are the full hand calculations produced by SkyCiv Beam:
SkyCiv Beam Software
Through this article, you have learned the concept of reaction forces at the supports and how to calculate support reactions. SkyCiv Beam Analysis Software allows users to analyze beam structures easily and accurately. You can get an analysis of your beam member, including reactions, shear force, bending moment, deflection, stresses, and indeterminate beams in a matter of seconds.
If you want to give it a try first, Free Beam Calculator is a great way to start, or simply sign up for free today!